二分查找算法详解 - LeetCode 704/35/34/69/367 题解
LeetCode 704.二分查找
题目描述
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入:
nums = [-1, 0, 3, 5, 9, 12],target = 9
输出:4
解释: 9 出现在nums中,并且下标为 4
示例 2:
输入:
nums = [-1, 0, 3, 5, 9, 12],target = 2
输出:-1
解释: 2 不存在nums中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
思路
二分查找是一种在有序数组中快速定位目标值的算法,核心思想是每次将搜索范围折半,直到找到目标或范围为空。该题强调了数组中无重复元素,一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的。后面我们会看到在有重复元素的有序数组中如何使用二分查找。
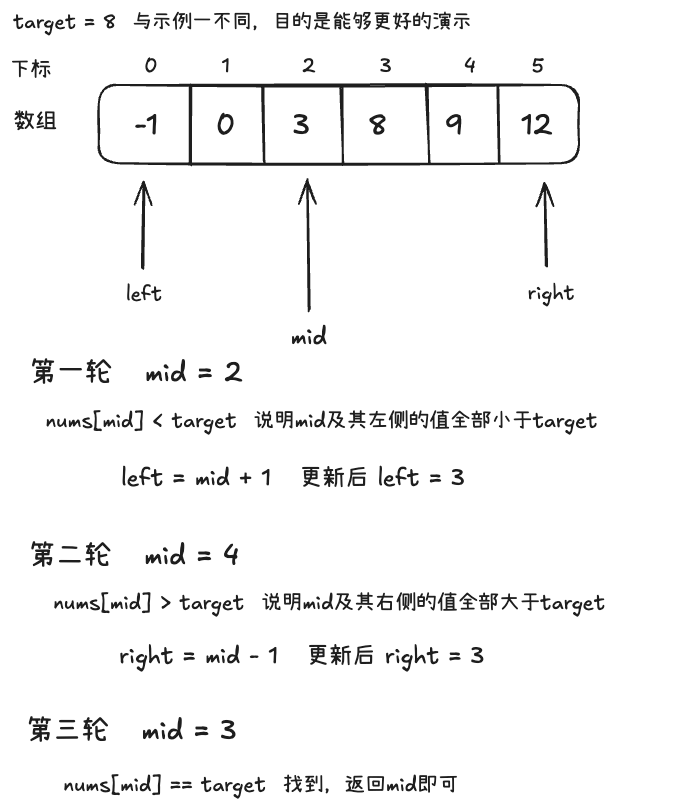
算法基本步骤(模版)
初始化左右指针:
left = 0,right = nums.size() - 1循环搜索:当
left <= right时:- 计算中点:
mid = left + (right - left) / 2 - 比较中点值
nums[mid]和目标target- 若相等,返回
mid - 若
nums[mid] < target,说明目标在右侧,移动左指针:left = mid + 1 - 若
nums[mid] > target,说明目标在左侧,移动右指针:right = mid - 1
- 若相等,返回
- 计算中点:
若循环结束仍未找到,返回
-1
C++代码
1 | class Solution { |
- 时间复杂度:
O(log n) - 空间复杂度:
O(1)
LeetCode 35.搜索插入位置
题目描述
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入:
nums = [1,3,5,6],target = 5
输出:2
示例 2:
输入:
nums = [1,3,5,6],target = 2
输出:1
示例 3:
输入:
nums = [1,3,5,6],target = 7
输出:4
提示:
$1 \leq \text{nums.length} \leq 10^4$
$ -10^4 \leq \text{nums[ i ]} \leq 10^4$
nums为 无重复元素 的 升序 排列数组$ -10^4 \leq \text{target} \leq 10^4$
思路
根据上一题,如果题目要求是在排序数组中寻找是否存在一个目标值,那么直接利用二分法可在 O(log n) 的时间内找到是否存在目标值。但这题还多了个额外的条件,即 target 如果不在数组中的时候需要返回按顺序插入的位置。我们只需要对二分法的标准模版稍作修改即可。
假设需要插入的位置是 pos ,则一定满足:
$$
\text{nums[pos-1]} < \text{target} \le \text{nums[pos]}
$$
因为数组 nums 为无重复元素的升序数组,所以数组中最多只会有一个元素等于 target 。
问题可以转化为:找到数组中找到第一个大于等于 target 元素的位置。
问题转化到这里,直接套用二分法即可,不断用二分法逼近查找第一个大于等于 target 的下标 。
C++代码
1 | class Solution { |
- 时间复杂度:
O(log n) - 空间复杂度:
O(1)
LeetCode 34.排序数组中查找元素的第一个和最后一个位置
题目描述
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:
nums = [5,7,7,8,8,10],target = 8
输出:[3,4]
示例 2:
输入:
nums = [5,7,7,8,8,10],target = 6
输出:[-1,-1]
示例 3:
输入:
nums = [],target = 0
输出:[-1,-1]
提示:
$0 \leq \text{nums.length} \leq 10^5$
$ -10^{-9} \leq \text{nums[ i ]} \leq 10^9$
nums是一个非递减数组$ -10^9 \leq \text{target} \leq 10^9$
思路
最简单的方法是从前往后遍历一遍。用两个变量记录第一次和最后一次遇见 target 的下标,但这个方法的时间复杂度为 O(n),不符合题目要求,没有利用到数组升序排列的条件。
根据题目意思,其实要找的就是数组中 第一个大于等于 target 的位置和 最后一个小于等于 target 的位置。这句话看似是一句废话,但实际上暗示了我们可以用 二分查找来解决这个问题。
可以通过两次二分查找来实现:
- 第一次二分查找:寻找第一个 大于等于
target的位置(即star) - 第二次二分查找:寻找最后一个小于等于
target的位置(即end)
这样,我们就可以在 O(log n) 的时间复杂度内找到目标值的起始和结束位置。
需要注意的是,在查找完成后还需要判断一下结果是否合法:即判断找到的位置是否真的等于 target,否则说明数组中不存在该值,应返回 [-1, -1]。

C++代码
1 | class Solution { |
- 时间复杂度:
O(log n) - 空间复杂度:
O(1)
LeetCode 69.x的平方根
题目描述
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意: 不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:
x = 4
输出:2
示例 2:
输入:
x = 8
输出:2
解释: 8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
- $0 \le {num} \le 2^{31} - 1$
思路
根据题目意思,最终的结果 ans 就是满足 $k^2 \le x$ 的最大 k 值。
所以我们对k可以进行二分查找,二分查找的初始区间就是 [0, x] ,只需要比较中间元素 mid 的平方与 x 的大小关系,并通过比较的结果调整上下界的范围。
所有的运算都是整数运算,不会存在误差,因此在得到最终的答案 ans 就是需要返回的结果。
C++代码
1 | class Solution { |
- 时间复杂度:
O(log x) - 空间复杂度:
O(1)
LeetCode 367.有效的完全平方数
题目描述
给你一个正整数 num 。如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
完全平方数 是一个可以写成某个整数的平方的整数。换句话说,它可以写成某个整数和自身的乘积。
不能使用任何内置的库函数,如 sqrt 。
示例 1:
输入:
num = 16
输出:true
解释: 返回 true ,因为 4 * 4 = 16 且 4 是一个整数。
示例 2:
输入:
num = 14
输出:false
解释: 返回 false ,因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。
提示:
- $1 \le {num} \le 2^{31} - 1$
思路
因为 num 是正整数,若 num 是有效的完全平方数,有 x * x == num ,则 x 一定满足 $1 \le {x} \le num$。于是可以将 1 和 num 作为二分查找搜索区间的初始边界。
根据题目意思,最终的结果 ans 就是满足 $k^2 \le x$ 的最大 k 值。
所以我们对k可以进行二分查找,二分查找的初始区间就是 [0, x] ,只需要比较中间元素 mid 的平方与 x 的大小关系,并通过比较的结果调整上下界的范围。
所有的运算都是整数运算,不会存在误差,因此在得到最终的答案 ans 就是需要返回的结果。
C++代码
1 | class Solution { |
- 时间复杂度:
O(log n),其中n为正整数num的最大值。 - 空间复杂度:
O(1)




